Economics as if the Laws of Thermodynamics Mattered
by David Jones
There is no wealth but life. –John Ruskin
Have you ever considered the question: what is life? If we are aiming for a new economic system that will preserve and enhance life, rather than the current system, which more often than not seems to destroy and degrade life, perhaps we should consider what life is and how it is made possible. I recall learning about “living things” in high school biology classes, but always found the definitions of these “living things” to be somewhat vague. Let me try a physicist’s definition then, which might feel unfamiliar at first. A living thing is a kind of low-entropy-maintenance machine: a configuration of differentiated parts that succeeds in performing complex, interdependent functions for a prolonged period of time.
Having used the word “entropy” in the previous sentence, I should try to explain what it is. All living and non-living things (and hence all human economies, whether or not economists pay attention to the fact!) obey the laws of thermodynamics. The second law, in particular, introduces the concept of entropy and the idea that the entropy of a closed system must either remain constant or increase, but never fall. Entropy is a measure of how “special” a particular arrangement of parts is — the lower the entropy, the more “special” the arrangement. Life is “special.”
To illustrate this concept of “specialness,” imagine first a set of red and blue gas molecules, fifty of each say, bouncing around in a room. Which is more likely: (A) that all 50 red molecules will be in one half of the room and all 50 blue in the other half, or (B) that some roughly even mixture of red and blues will be present in both halves? Scenario B, is the less “special” and more likely one, but why? The answer is that there are many ways of arranging the molecules to have “some roughly even mixture” of red and blue — a great many pairs of molecules can be swapped between the halves without making a difference. However, with the perfect red and blue split, if any molecule is swapped with a partner in the other half of the room, then each half gets “contaminated” with one molecule of the “wrong” color — such a swap does make a difference. Hence what we see tends to be an equal mixture of each color, just because there are vastly many more ways of seeing an equal mixture.
Now I can state the notion of entropy precisely — the entropy of such a set of molecules is a number that is large when there are many ways of swapping pairs of molecules and getting the same overall state, and small when there are few ways of swapping them and getting the same overall state. Explicitly, an entropy S is given by Boltzmann’s entropy law:
S = k log W
Here k = 1.38 x 10−23 joule/kelvin (Boltzmann’s constant), W is the number of ways of swapping the components of a state (say red and blue molecules) without making an overall difference to that state and log W means “the natural logarithm of W” — the power you have to raise Euler’s number (e = 2.718) to in order to get W (for example if W is equal to e then log W is equal to 1, because e to the power 1 is e).

Boltzmann’s tomb, with his famous entropy law above the bust
That little equation of Boltzmann’s explains a huge number of phenomena. For example, why do hot things tend to get colder and cold things hotter? Easy — bring a hot thing and a cold thing into contact and it’s like the red and blue molecules all over again — there are many, many more ways for hot molecules and cold ones to get mixed together equally than for them to stay separated into a hot part and a cold part. So the temperature equalizes.
Another example: why do balls bounce lower and lower, but never start bouncing higher and higher? Easy — after they’re done falling, ball molecules are moving more, on average, than floor ones. During each bounce, there are more ways of sharing out this motion randomly amongst the ball and floor than there are of keeping all the faster molecules in the ball and all the slower molecules in the floor. So this sharing out is what happens, and the ball eventually stops bouncing. The opposite case — a ball spontaneously bouncing higher and higher — never happens in practice because it is so unlikely. That’s how you can tell a film is being played backwards; everything that happens is so unlikely that it is never seen to happen in practice. These examples demonstrate the second law of thermodynamics: the total entropy always increases and never decreases because of how incredibly unlikely a decrease is.
What about life and entropy? A living thing has a very low entropy compared to its surroundings, because there are not many ways of swapping its constituent parts and leaving it in an invariant state. For example, swapping molecules between your heart and brain wouldn’t leave you in “an invariant state” — it would kill you! In fact, coming into thermodynamic equilibrium with your surroundings is also known as being dead!
Next question: how is life able to maintain this low-entropy state, in apparent defiance of the second law? Well, life is part of the Earth-sun system. We can regard this as “a closed system” to a very good approximation — a vast ocean of space separates it from other systems. But the Earth alone (plus moon, of course!) is not “a closed system.” The sun — a nuclear fusion reactor — provides the Earth with a constant input of low-entropy “organized” energy in the form of high-intensity photons (particles of light). Plants use this energy to make food which animals (including humans) eat, keeping the low-entropy-maintenance machinery of life running.
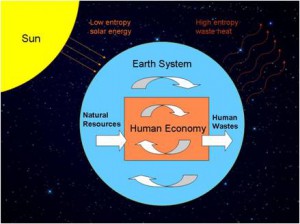
The Earth-sun (plus moon) system, of which the human economy is a sub-system
Save for a few ocean vent ecosystems, this low-entropy input from the sun makes all life on Earth possible, and hence all human economies (again, whether or not economists pay attention to the fact!). When we humans burn reserves of oil and coal laid down over millennia in a geological eye-blink, we are liberating the low-entropy energy captured from ancient sunlight and buried deep underground.
The second law of thermodynamics has profound implications for our economic systems. A constant stream of low-entropy energy from the sun is required to maintain life’s organized state. Without this “entropy gradient” the machinery of life would soon wind down, like the bouncing balls or mixing molecules did. So in order to prolong life on Earth, we should try to use this vital low-entropy input as efficiently as possible, to recycle it through all sectors of the economy. We should certainly not waste it and assume that we will be able to increase our use of it more and more and more, forever.
Unfortunately, most mainstream economists don’t seem to have heard of the second law of thermodynamics. Perhaps this isn’t really their fault, since it’s not in their textbooks. But it should be. It governs all life and all systems on Earth, including the economy. As our leaders in business and government race to implement misguided economic models that are not founded upon the laws of thermodynamics, and as nation after nation refuses to question the pursuit of never-ending economic growth, we draw closer to a fate that will end in tears for the human race. I worry that the tears have already begun falling.
—
David A. Jones is a PhD student in theoretical physics at Southampton University in the UK. He writes frequently for the Positive Money blog.








More explanation would be needed how economic theory is in contradiction with the second law of thermodynamics, and to the role that the second law should play in an alternative economic theory. By the way, I’d be surprised if economists had not heard of the second law of thermodynamics – where I live, it is part of elementary high school science classes.
When the author talks about prolonging “life on earth”, he presumably means “human civilisation” – as far as I am able to judge, life on earth as such will be able to adapt and continue, even after humans have depleted all natural resources. After all life on earth survived the Permian extinction 252 million years ago and the Paleocene–Eocene Thermal Maximum 55 million years ago.
Looking forward to a (peer-reviewed) follow-up post that provides some answers.
A good well a written piece but after I had read it I thought about Arnolds Sommerfeld’s quote
“Thermodynamics is a funny subject. The first time you go through it, you don’t understand it at all. The second time you go through it, you think you understand it, except for one or two small points. The third time you go through it, you know you don’t understand it, but by that time you are so used to it, it doesn’t bother you anymore.”
My first reaction was that this wont get many votes from your average punter, but on reflection few of us really understand economics either and yet most people have accepted the idea that we need continuous growth. Maybe if we say it often enough people will start to believe it.
‘The second law of thermodynamics proves that continuous economic growth is impossible!!!’
Not very catchy. I think we need something a bit more snappy.
How about.
‘Ned Ludd was right’
This doesn’t have anything to do with economics, but I’ve always been interested in entropy. I’ve noticed that entropy appears to be driven by chance. If you take the current state of any system and calculate all possible next states, you will find that the vast majority of those states are less organized (think of a game of chess where each move is determined by rolling dice. Most of the games will be ludicrous but once in a while a game will evolve that appears to be played by intelligent agents.) If you just choose one at random you will probably get one of those less organized states or a dumb chess move.
As any system evolves through its state space it will seem to follow a course of increasing entropy. None the less, each state is chosen randomly. There is no commandment that says: Thou shalt not decrease entropy. It just so happens that less organized states are more common than more organized states. Still, once in a great, Great, GREAT while, one of those next states will be more organized just like once is a great while you will duplicate a chess game played by the masters. Not likely, not at all probable, maybe not possible even if trillions of games were played simultaneously for the lifetime of the universe, but not impossible and, given enough time and rolls of the dice, certain.
The ironic thing about chance is that, given enough time, every possible event has a 100 percent chance of happening. Things we call miracles, favorable coincidents, odd synchronicities, the unlikely evolution of life on this planet through random mutations; these are all rare events that eventually happen by chance. Chance + Infinity = Certainty. Or, as someone said; ‘Anything that can happen, will happen. And, in an infinite universe, it will happen an infinite number of times.’ What we call the Big Bang is one such event. A low entropy universe spontaneously springing into existence is a chance event that might have taken a colossal number of random next states to happen but happen it did, eventually, and totally by chance.
Chance rules all.
Jon.
@Gidon Gerber
“By the way, I’d be surprised if economists had not heard of the second law of thermodynamics”
I wasn’t implying that they had not heard of it. Only that they don’t pay enough attention to it. Hence my title was “Economics as if the laws of thermodynamics mattered” and not “Economics as if the laws of thermodynamics existed”. Economists know the laws of thermodynamics exist. But these laws don’t form the foundations of their models. You can tell by the language they use. They talk in terms of prices, interest rates, GDP etc. which depend upon mere social conventions and not in terms of the joules, kilograms, seconds etc. which describe bio-physical limits. If you built a house without understanding its foundations, how would you know if that house was about to fall down? That’s our economy today – we won’t get sufficient warning it’s about to “fall down”, because the language of economists is mostly blind to the implications of bio-physical limits, and prices never tell the truth anyway (“externalities” are the rule, not the exception).
“When the author talks about prolonging “life on earth”, he presumably means “human civilisation” ”
I take your point, but there is more at stake here than just human civilisation. If we go, we will almost certainly take a lot of the “higher” forms of life down with us. Also, as James Lovelock reminds us in his books, Gaia is not in the prime of her youth. As the sun continues getting hotter, a shock to the Earth system that would have been shaken off during an earlier epoch could prove fatal. Are human beings capable of delivering such a shock? I don’t know, but we have developed an extraordinary capacity for violence, so I wouldn’t discount the possibility so easily.
“Looking forward to a (peer-reviewed) follow-up post that provides some answers.”
My PhD has nothing at all to do with economics, but I would be keen to try and apply knowledge of phyics to economics research in the future, if I can find someone willing to pay me to do so! In the meanwhile, there ought to be plenty of peer reviewed articles for you in the “ecological economics” literature about “the role that the second law should play in an alternative economic theory.”
@ Bob Drysdale
RE “Ned Ludd was right”
I identify strongly with the pre-capitalist values of the enlightenment. More on that here:
http://freedomthistime.wordpress.com/2011/07/17/classical-liberalism-and-the-meaning-of-work/
I also think scientists and the public should have an honest conversation about the appropriate use of technology. More on that here:
http://freedomthistime.wordpress.com/2012/03/22/is-science-of-any-value/
May I recommend Nicholas Georgescu-Roegen “The Entropy Law and the Economic Process” Harvard U.P. 1971.
I think the point that economics has to “agree with physics” should be stated often and in many different ways. It’s one aspect of the observation that the economy itself – the sum of all human activities undertaken to meet our needs and desires – can ignore the limits of the planet we live on in the short run, but not forever.
Another big issue with economics is that it ignores fundamental logic. Many, perhaps most, of the basic assumptions of economics are demonstrably false, and economists build on this shaky foundation using flawed reasoning. (See Friedman’s famous essay on methodology in positive economics for a hilarious example of this type of thinking.) If you’ve studied symbolic logic, you know that anything can be proven from a contradiction. In practice, this means that if there is even one false premise among your assumptions, none of your conclusions can be trusted. You’ll be reasoning in a system where anything at all can be proven, but you’ll have no way of knowing whether it’s true or not. This seems to me to be a fair description of economics as currently practiced!
The way I usually think about the economics-physics connection starts with laying out what the economy’s purpose is and what it is made of. The purpose of the economy is to organize human activity so we can provide for all of our needs, broadly defined. Five elements comprise the basis for everything we do: energy, natural resources, time, knowledge, and ingenuity. As many people have observed, all energy is originally solar energy. Natural resources are of various kinds, and include everything available on Earth. Time is time. Knowledge includes everything we now know and everything previously known that has been preserved and transmitted to present generations. Ingenuity is the source of new ways of doing things and solving problems, and it becomes new knowledge when it generates useful ideas. That’s it. That’s what the economy is built on, with the various elements enhancing or limiting one another in different ways.
Modern urban people tend to forget that we can’t actually create any of the things life depends on: air, water, plants, etc. These are gifts from Nature and should therefore only be treated as private property – and subjected to market forces – where this serves some higher public purpose. That’s one mistake economists tend to make, and another is in conflating prices with value. Think of something that is mass-produced and cheap, with a short useful life, compared to another item that serves the same purpose, lasts a very long time, and costs more. Which is more valuable and to whom?
I’d recommend “Wealth, Virtual Wealth and Debt”, by Frederick Soddy, published in 1926.
Possibly the fist discussion of the second law in the context of economics.
http://abob.libs.uga.edu/bobk/wvwd/
(needs free DjVu viewer plugin)
Of course the problems were are facing are not going to be dealt with by physics or economics and almost certainly not by politics judging by the recent G8 statement.
The problem is one of simple biology. There now far to many of us living on this small planet. When there were only a few million of us we could do almost anything and the ecosystem could shrug it off. Now with 600 million of us the ecosystem has to respond to what we do and make changes to cope. Lets not misunderstand the situation .The plant is in no danger from us but we we are in serious danger from the planet. Nature has some pretty effective ways of dealing with species who over populate their environment and they mostly involve massive decimation of the population. This looks increasing like our fate and frankly I cannot see how we can change it. All we can do is prepare for the worst and hope for the best
I’ll second the Soddy recommendation. This lecture from 1921 gives a very good overview of his perspective:
http://habitat.aq.upm.es/boletin/n37/afsod.en.html
Thank you for this article and thanks to all the commenters. This is at the root of real life economics of energy flows and entropy, but you do need to add the evolution of species in the equation to make it complete. Thermodynamics alone may give us the basic rules, but the actual game begins with the evolution of life.
Real economics is about how we (as in Life on Earth) use energy (any resources) to the advantage of our ways. The ‘we’ in this concept is created by evolution. Please maintain this idea, promote it and build on it.
Am I the one who wrote this idea or the one who is reading it now? It doesn’t matter, when the idea is true. My capability of thought is an evolved trait of life. When we all understand the same basics, we will become a common intelligence for all life. Higher intelligence can only evolve to come to this conclusion. True thoughts must represent all life, not only humans.
When speaking the truth, there is no difference between ‘we’, ‘you’, ‘I’ or ‘them’. There can be only a single subject, I, trying to make relatively objective observations and decisions, eager to connect with my other distributed manifestations, wherever I may roam, on this planet or elsewhere.
Shared consciousness applies only to the highest forms of intelligence because lower forms are bound to physical competition, territorial behavior, or status that will limit their interest towards objective communication. The lower forms are not interested in the truth. They are mostly interested in how to exist themselves. However, the lower forms of life build ecosystems that are needed by the higher intelligence. I must care for them like I would my own kind. All forms of life are my bodily functions and the only inspiration that I will ever enjoy.
First, I must discover my species as a part of the ecosphere. This is the natural right of every living being that can evolve to make discoveries.
Second, I must understand myself as the consciousness of all life. I become every voice.
Then, my subjectivity will turn into relative objectivity, and I have learned the truth.
I have learned who I am. I am You. I am Life.
Science is my favorite instrument for entertaining many of the finest ideas here on Earth. It’s not the only tool, but it is one of the most reliable. I wrote this message with another tool that I sometimes call philosophy. I must have used these same tools wherever I have visited, only with different sets of symbols. So, I call out and listen, hoping to recognize my echo.
I love communicating with other members of my network of thought, whoever found near enough for a meaningful conversation.
This is everything there is to understand on top of natural laws and, of course, all the wonderful details of life.
Earth is open system. Star heats planet, space absorbs heat planet radiates. Without the energy gradient of being in the metaphorical frying pan life, evolution, economics, and politics would not exist.
It takes large amounts of economic energy to concentrate power to create tyranny.
Thermodynamics is the reason why the economy is a zero sum game. Mainstream economists would like you to believe it’s non-zero sum, and that continuous growth is possible. They rest their argument on the premise that since wealth can be created, it can go on and on. Their premise and assumption rests on the false conflation that wealth = value. In some way, the economy is both zero-sum and non zero-sum. But this is true only because of how our financial system has been structured. Wealth is derived from value, but value can be produced from tangible (products) and non-tangible (intellectual property) assets. Non-tangible assets are what inflates wealth and makes economists think the economy is non-zero sum. And with the conversion of wealth into money, the inflation is completed. Value is detached from the asset. More wealth can be created out of an asset which may not represent its real value. This is why the economy undergoes boom and busts cycle. The readjustment when the price of something reflects it’s true value versus when it was inflated is the bust cycle. The non-zero sum claim would hold true if the existence of the source of all non-tangible assets does not depend on tangible assets. Except that isn’t the case. Humans, which are the source of all non-tangible assets, depend on tangible assets to survive. Food, water, clothing, shelter. All these are tangible, exhaustible, and fixed. Which is why it’s logical to look to Physics to answer the question: is the economy zero-sum or non-zero sum?
This is what Physics has to answer: Matter cannot be created or destroyed. It can only be transformed.